
引子
本文将分析《》中第二个问题:设定值改变对微分项的影响。语文不好,原文中叫做Derivative Kick,实在是想不出好的名字,暂且称为微分冲击。
问题定义
既然叫做微分冲击,那么这个问题肯定和微分项有关,并且是微分项会受到一个突发状况的影响,产生一个较大的冲击,详见下图。
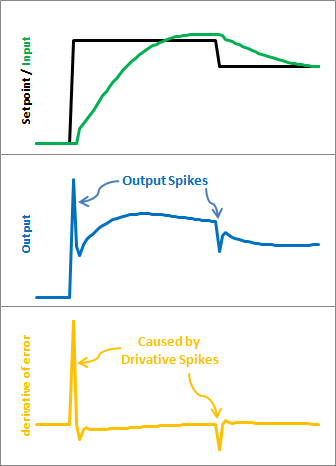
从第一张图看出,当设定值产生一个阶跃后,被控量Input随着时间慢慢向设定值靠近,第二张图反应的是设定值产生阶跃后控制量Output的变化,可以发现,Output会突然产生一个较大的阶跃,具体原因可以参考“万恶”的PID经典控制方程。第三张图描述的是Output的梯度(也就是变化率:值变化:时间变化),同样可以发现一个脉冲,并且这个脉冲可能会非常的大(dt非常小),远远超过Output变化量。同理,图中页描述了当设定值突然减小,Output及其对应的梯度变化情况。对于一般的系统来说,我们不希望这样的突变发生(可以想象如果采样周期很长,那么这个冲击会持续很长时间,系统估计就飞起来了)。当然如果你的系统需要这个冲击,那么这个问题就可以忽略,下面的解决方案也就不需要浏览。
解决方案
首先,感谢我们伟大的数学家,结合经典PID控制方程,来看一个公式:

Setpoint这一项就会产生一个巨大的冲击,而且仅会产生一次,在下一个计算周期就会消失。处理的方法很多,最简单的就是讲Serpoint这一项移除,也就是认为对于微分项来说不存在设定值的改变。如果这么处理,系统会不会失控呢?这种玩法已经和我们根深蒂固的经典PID理论不一样了啊!!这怎么整!
上述问题的答案是不会,我们将上述过程写成数学表达式:
用Input变化量取反来代表Error的变化(其实就是忽略Setpoint的变化)。这里不讨论经典的PID控制方程,我们的目标是使Input根据Setpoint往我们预计的方向靠拢,上述做法无可否认,与经典PID方程不一致,但核心思想是一致的。由于Setpoint变化仅对Output产生一次影响(也就是产生了那个尖峰),一旦步入一下个计算周期,Output就不在收到Setpoint变化的影响,回归正常,不影响PID调节(具体影响图示,请参照文末)。
代码
/*working variables*/unsigned long lastTime;double Input, Output, Setpoint;double errSum, lastInput;double kp, ki, kd;int SampleTime = 1000; //1 secvoid Compute(){ unsigned long now = millis(); int timeChange = (now - lastTime); if(timeChange>=SampleTime) { /*Compute all the working error variables*/ double error = Setpoint - Input; errSum += error; double dInput = (Input - lastInput); /*Compute PID Output*/ Output = kp * error + ki * errSum - kd * dInput; /*Remember some variables for next time*/ lastInput = Input; lastTime = now; }} void SetTunings(double Kp, double Ki, double Kd){ double SampleTimeInSec = ((double)SampleTime)/1000; kp = Kp; ki = Ki * SampleTimeInSec; kd = Kd / SampleTimeInSec;} void SetSampleTime(int NewSampleTime){ if (NewSampleTime > 0) { double ratio = (double)NewSampleTime / (double)SampleTime; ki *= ratio; kd /= ratio; SampleTime = (unsigned long)NewSampleTime; }} 代码用Input的变化取代了Error的变化。
结论
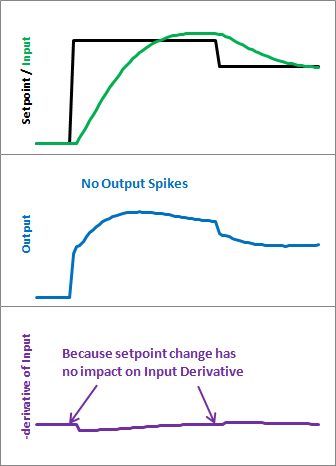
- Output梯度尖峰被去除
- 控制量原来存在一个尖峰被消除
- 被控量的微分变得较为平坦
NOTE:如有不足之处请告知。^.^
下一章将介绍如果在系统运行过程中,突然改变PID控制参数对系统的影响
PS:转载请注明出处: